(작성중....)
Transformer Interpretability Beyond Attention Visualization
github.com/hila-chefer/Transformer-Explainability

Vision transformer에서 relevance score를 계산하는 방법을 제시하는 논문
Method consists of 3 phases:
|
원리는 LRP처럼 Deep taylor decomposition 기반으로 local relevance를 할당하며, layer를 통해 전파한다. 그런데 여기서의 propagation은 attention layer, skip connection (가장 챌린징한 부분임) 을 포함하고 아마 여기서 의미가 있는 듯하다.
layer끼리의 total relevance가 유지되기 위해 어떤 테크닉을 사용했는지 살펴볼필요가 있다. 최근 연구인 visual transformer 기반으로 분석을 진행했고 text뿐아니라 다른 XAI기법들과도 비교되었음
그럼 시작에 들어가기 앞서, transformer를 되짚고 가야함. transformer의 main block은 self-attention layer로 되어있는데 두 토큰 사이에 pairwise attenton이 이루어진다. NLP에서는 token이 보통 한 단어이고 비전에서는 이미지 패치이다.
Attention에서 일어나는 일들을 해석하기 위해 여러시도들이 있었던 것 같음.
간단하게 각 토큰으로부터 얻은 attention을 그냥 평균하면 시그널이 bluring되거나 혹은 레이어의 각 다른 역할들을 고려하지 못하게됨.
Rollout method라는 것도 있는데(이것도 2020년), 모든 attention score를 pairwise attention을 고려하면서 재할당하고, attention이 연속적인 컨텍스트로 linearly 결합됨을 가정한다.
그러나 이제까지는 간단한 가정에만 의존하였고 종종 highlight되는 토큰과 관련이 없었던 듯.
본 연구에서는 relevance 합이 레이어를 통해 유지되면서 propagate되는것을 기본적으로 하되,
Transformer는 크게 skip connection과 attention operator에 의존하므로 두 activation map을 모두 mixing하는 것이 매우 챌린징했음. 더군다나 transformer는 non-linerairty라서........ㄷㄷ RELU처럼 positive, negative 값 얻을수없다
심지어 non-positive일때 skip connection에 이끌리면 엄청난 불안정을 겪을 수 있다.
이렇게 챌린징한 부분을 이들은 어떻게 해결했는가!
|
1) positive와 negative에 쓰일수있는 relevance propagation rule 사용. 2) skip connection같은 곳에는 non-parametric layer를 위한 normalization term을 둔다. 3) attention과 relevancy score를 통합하고 통합된 결과를 결합해서 multiple attention block을 만든다. |
<Related Work>
- Explainability for computer vision : LRP, Integrated grad, grad CAM, RAP, DeepLIFT 등
- Explainability for Transformers
일반적인 모델들에 비해 vision transformer에 대해서는 contribution이 많이 없다. LRP도 트랜스포머에 이용됬었는데, relevance score가 input까지 propage되지못하여 각 head까지 relevance가 가지 못하는 한계등이 있었음
| We note that the relevancy scores were not directly evaluated, only used for visualization of the relative importance and for pruning less relevant attention heads. |
그래서 이 논문에서는 과거에 relevance score(R) 이 바로 계산되지 못하고, 덜 연관된 attention head를 프루닝 or relative importance를 시각화하기 위해서만 사용된것에 대해 주목했음
3. Method
Transformer에서 각 layer의 Attention head에 대한 score를 계산하기 위해, LRP 기반의 relevance propatation을 이용했음. Relevance score랑 Gradient 값을 모두 통합함으로써 반복해서 negative relevance는 제거하는 방식으로 하였고, Attention graph 에 해당하는 이 score들을 통합한다.
3.1. Relevance and gradients
class t에 대응하는 relevance와 gradient를 propagate 한다.
| $C$ | Class |
| $t$ | 시각화될 class 인듯. |
| $L^(n)$ | n번쨰 layer |
| $x^(n)$ | n번째 layer의 input |
| $x^(N)$, $x^(1)$ | network input, network output |
| ${{L_{i}}^{(n)}}(X, Y)$ | n번째 layer의 operation이며, feature map 및 wegiht를 뜻함 |
| R | Relevance |

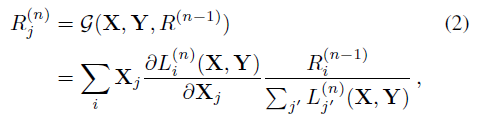

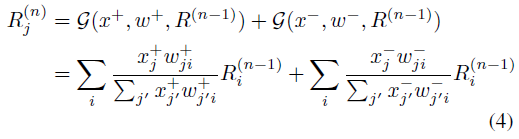
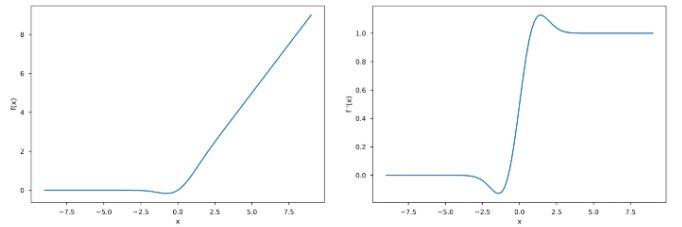
ReLU와 다르게 GELU같이 -/+ output이 가능한 것들은 conservation rule (Eq 3)이 깨진다는 것에 주의한다.
-/+에 대한 각 sum이 독립적으로 normalize되기때문에
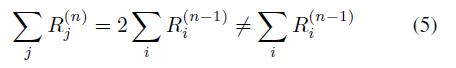

Eq(4)가 conservation rule을 만족하지 않음을 언급한 반면, Eq(6)은 +/- input에 모두 만족한다.
3.2. Non parametric relevance propagation:
Transformer 모델에는 학습된 tensor가 있는 feature map과는 반대로, 2개의 feature map tensor가 섞여있다.
-> Skip connection과 Matrix multiplication (Attention module)
1) Skip connection
2) Matrix multiplication

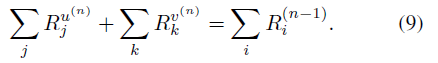
Lemma 1. u, v tensor이 있고, Eq(1)에 따라 계산되는 Relevance를 고려함

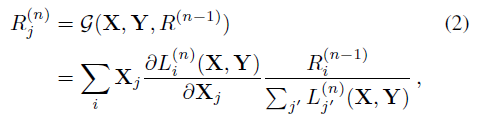
위 Eq(2)처럼 u,v tensor계산을 할 때, matrix multiplication 하면 Eq(2)는 Hold되지 않는다. Add layer에서는 u와 v가 서로 독립적이지만, matrix multiplication에서는 서로 연결되기 때문이다.
Skip connection의 Relevance를 전파할때, 수많은 불안정성에 마주하게 된다. 추가 operator 의 conservation rule에 의해, Relevance score 합이 상수인??
Lemma 2. normalize된 Relevance score R^u와 R^v는 다음 특성을 가짐
i) conservaton rule이 유지되며, 각 텐서의 합의 Relevance

3.3 Relevance and gradient diffusion
3.4 Obtaining the image relevance map