'Empirically' 이라는 단어가 많이 나오는 논문이다. 짧게 요약하자면! 저자는 총 3가지 분석을 했다.
1. Classificaion region 영역의 특성 : 한 region이 다 연결되있음..
2. Decision boundary의 curvature(곡률)특성 : 곡률이 거의 평평한데 주요 몇(?)개 곡률이 그렇지 않음. 이 현상은 original sample과 perturbed sample이 방향이 다름.
3. 위 현상으로 알고리즘 제시 : 위 현상 이용해서 좀 더 robust network를 만드는 알고리즘을 제시하자~
perturbed sample은 decision boundary가 + 쪽으로 싸고 있고, original sample은 decision boundary가 - 쪽으로 싸고 있는 현상을 우리는 발견했다. curvature의 principle component를 다 더했더니 이러한 현상을 발견한것이다. 따라서 이런 특성을 이용해서 decision boundary에 대한 curvature방향으로, 이 샘플이 orignal인지 pertrubed인지 더 잘 구분하는 더 robust한 network를 만들자.
<자료를 영어로 만들어서 영어로 첨부함>

















<introduction>
While the geometry of classification regions and decision functions induced by traditional classifiers (such as linear and kernel SVM) is fairly well unㅎderstood, these fundamental geometric properties are to a large extent unknown for
state-of-the-art deep neural networks. Yet, to understand the recent success of deep neural networks and potentially
address their weaknesses (such as their instability to perturbations [1]), an understanding of these geometric properties remains primordial.
-> classification 영역과 decision boundary의 기하학성은 전통적인 classifier로부터 유도된다. 그러나 sota 뉴럴넷들에 대한 근본적 특성은 아직 알려져있지 않다. 그러나 뉴럴넷 성공을 이해하고 잠재적으로 그들의 취약성을 알아내기 위해 기하학적 특성의 이해는 원시적으로 남아있다.
In this paper, we specifically view classification regions as topological spaces and decision boundaries as hypersurfaces, and we examine their geometric properties. We first study the classification regions induced by state-of-the-art deep networks, and provide empirical evidence suggesting that these classification regions are connected; that is, there exists a continuous path that remains in the region between
any two points of the same label. Up to our knowledge, this represents the first instance where the connectivity of
classification regions is empirically shown. Then, to study the complexity of the functions learned by the deep network, we analyze the curvature of their decision boundary
-> 해당 연구에서, 우리는 topology space 및 decision boundary로서의 classification 영역을 주로 볼것이다. 그리고 그들의 기하학적인 특성을 관찰한다. 먼저 1) classification regions (sota 뉴럴넷들로부터 유도되는) 을 보고, 2) 경험적 증거를 제공한다. 즉 same label이지만 두 data point일때의 관계를 보는 것임
-> 우리가 이해하기로는 이 영역이, classification regions의 연결성이 경험적으로 보여지는 곳이라고 본다.
-> 그리고 뉴럴넷으로부터 학습되는 function들의 복잡성을 연구하기 위해 decision boundary의 curvature를 분석한다.
<Contribution>
- Natural image 부근의 decision boundary는 대부분의 방향에서 평평하고 아주 극소수의 curved된 방향이 존재함을 관찰했다.
- 뉴럴넷의 decision boundary에서 근본적으로 비대칭이 존재함을 밝혔고, 그로 인해 decision boundary는 negative curvature 방향으로 biased되게 됨을 보였다.
- curved된 decision boundary의 방향은 다른 datapoint 사이에 공유된다. -------> 이거 아직ㄷㄷ
- input에 purturbation주었을때의 classifier의 민감도와 shared 방향 사이의 관계가 존재함을 증명한다.
- 이러한 방향을 따라 purturbation을 주는게 가치가 있으며, 다른방향을 따라 purturbation주게 되면 덜 민감하다.
본 연구로 인해 밝혀낸, 뉴럴넷의 근본적인 비대칭 특성을 잘 활용하여, natural image를 detect하는 알고리즘을 제안한다. 또한 perturbed된 image의 올바른 label을 평가하는 방법도 포함한다.
<Notation>
| $\hat{k}$$(x_0)$ | estimated label by $argmax_k f_k(x_0)$ |
| $f_{k(x)}$ | K th component of f(x) corresponds to k class |
| set B | {Z : F(Z) = 0}, where ${f_{i(z)}}$ = ${f_j(z)}$ between i and j class, the pairwise decision boundary |
| Path P | represented as a finite set of anchor points. |
3. Topology of classification regions

The author starts this question!
Do deep networks create shattered and disconnected classification regions, or on the contrary, one large connected region per label (Fig. 1a)?
저자는 이런 물음으로 시작한다. classification 영역이 끊어진채로 흩뿌려져 있을까 혹은 하나로 크게 연결되있을까? 아직 unclear 하오나 여기에서 그들은 하나의 영역이 있다고 보고 path의 연결성을 연구한다.
they treat $R_{i}$ as topological spaces, and their path connectness.
두 data point가 있을 때, 같은 class 영역에 놓여졌다고 하면, continuous한 curve가 있을까? 이 문제를 증명하기엔 꽤 까다로우므로 they propose a heuristic method to study this question. 휴리스틱한 방법을 제안한다.

1. To assess the connectivity of regions, they propose path finding algorithm between two data points.
2. To find this path, the algorithm attempt to take convex path between x1, x2 , and when the path is not entirley included in region, the path is modified by projecting the midpoint p = (x1+x2)/2
3. until the whole path is entirely in the region, same proceduere is applied recursibely on path (x1, p)
and (x2, p)
4. In practice, Path P의 validity is checked empirically through a fine sampling of the convex combinations of the consecutive anchor points.
1. 영역이 연결되있음을 평가하기 위해 두 데이터셋(x1, x2) 사이 path를 찾는 알고리즘을 제안한다.
2. 이 path를 찾기 위해, 해당 알고리즘은 x1, x2 사이 convex path를 찾는 시도를 하는데 만약 path가 region에 포함되지 않으면 x1, x2 사이로 projection해서 region에 들어오도록 수정한다.
3. 한 영역의 모든 path가 찾아질때까지 반복된다. 4. path P의 정당성은 convex combination 샘플링을 통하여 empirically 확인되었다. 그리고 실제로 샘플링된 지점 사이 거리를, 원본 두 이미지 사이의 거리보다 4배 더 작은 sampled point 로 정했다. 왜? 빨리 끝나라고 한거니?
암튼 위 방법은 imageNet classification에서 CaffeNet architecture connectivity를 평가하기 위해 사용되었다.
이것을 위해, 우리는 path의 존재를 검사했는데.. 아래 3가지 시나리오로 path검사를 한듯하다.
|
1. With the same estimated label, validation set, Two random sampled point. 2. One random sampled point(x1) from validation set and 1 perturbed image(x2), r is perturbation. $x_{2} = \tilde{x_{2}} + r$ , $\tilde{x_{2}}$ 는 x1과는 다르게 분류되었으나 r을 통해 x1과 같은 regison으로 분류됨 3. One random sampled point(x1) from validation set and perturbed random point. similar scenario 2 but, $\tilde{x_{2}} $ is just random image. |
두 이미지 사이 connectivity를 확인하였더니 시나리오 2,3에서 비쥬얼적으로 x2와 x1이 일치하지 않았지만, 이미지 시각적 특성과는 독립적으로, classification 영역의 지오메트릭 특성은 분석되었다.
In all scenario, they check connectivity between 2 images that have same estimated label. In scenario 2 and 3, x2 does not visually corresponds to x1. with this setting, geometric property of classification region are analyzed independently of visual property. (Fib 1b)
각 시나리오마다 1000개 pair로 실험했고, 위 알고리즘의 approach는 연결된 path를 찾기위해 사용되었다.
The result as follow.
|
1. 모든 시나리오에서, 동일 class region의 두 point 사이에서, 해당 영역을 포함하는 연결된 path가 항상 존재한다는 증거는 힌트를 준다. 2. Moreover, 두 point를 연결하는 연결된 path는 대충 straight path 이다. 직선의 path엿다....  $D(p) $\approx$ 1 $ 이렇게 해서 straight path 에 가깝다고 한다. 그리고 3개의 시나리오에서 average deviation이 1+10-4 , which is slight deviation from straight path.. |

두 pair point의 연결이 대략 straight path 임을 발견했지만, it is important to note that classification regions are not
convex bodies. (convex 가 아닌것도 있었나보군)


동일 class region에 속하는 k개의 이미지 조합이 많아질수록 같은 영역에 들어올 확률이 줄어감을 확인하였고 이것은 classification region이 Rd에서 convex body는 아니라는 것을 의미한다.
이 결과는 뉴럴넷 region이 그들의 분류 region을 두 이미지 사이에 approximately flat하게 extrapolate한다는 것이다. (예를 들면, 같은 class의 두 이미지 사이 near convex path가 존재함) 하지만 분류 region 전체는 convex body는 아니다. In simplistic 2 d world, this looks like fig 4.
convex combination
4. Curvature of the decision boundaries (Decision boundary의 굽음. 곡률)
The definition of curvature in this study:
K(z, v) is defined curvature of planar(평면) curve, cross-section of B along a tangent direction v set T ,

u: normal plane 초록색
The curvature can be expressed in terms of Hessian matrix.

주 방향은, 이 curvature 를 최대화하는 tangent space와 직교하는 방향으로 대응된다.
구체적으로, l 번째 principal direction $v_{l}$ 는 k(z,v)를 maximizing함으로써 얻어지는데,
(v_l, ...v_l-1 를 constraint로 두면서) 그렇지않으면, 주 curvature는 nonzero eigenvalue에 대응한다.

저자는 natural image 부근의 뉴럴넷 decision boundary의 curvature를 분석한다. CIFAR 10로 훈련된 LeNet 아키텍쳐로 분석하였으며 decision boundary의 principal curvature를 validation set의 랜덤 이미지 1000개 부근에서 보여주었음
구체적으로, image $x$ 에 대해서, perturbed image $z = x + r(x)$ 가 x와 가장 가까운 decision boundary에 대응한다는걸 보였다. (corresponds to the closest point to x on the decision boundary.)
따라서 저자는 Eq(1)에 따라 z point의 prinicipal curvature를 계산한다. 이 principal curvature의 계측 평균은 Fig 5b.
이 그래프가 의미하는건 무엇인가? 두 네트워크 모두, The large majority of principal curvatures are approximately
zero: along these directions, the decision boundary is almost flat.
남은 principal direction을 따라, decision boundary는 무시할수없을 정도의 positive or negative curvature를 갖고있었다. 흥미롭게도 principal curvature profile은 비대칭이었고 negative하게 굽은 방향을 향하고 있었다.
저자는 셋팅을 바꿔가며 이 비대칭성을 관찰했는데, like different datapoint/dataset/network... 이러한 특성은 실험환경마다 모두 동일함을 확인했다. (인공적인것이 아님) 다음 section에서는, Decision boundary의 비대칭성(natural image부근의)을 활용하여, clean image로부터 adversarial example을 감지하는 것을 알아보자.
위 분석은 Decision boundary가 구부러지는 방향이 거의 없음을 보이는데, 저자는 1) 이런 방향이 두 datapoint를 통해 공유되는지 조사 하고, 2) 이러한 방향이 뉴럴넷의 robustness와 관계가 있는지 조사한다.
1) Shared common curved directions :
Compute the largest principal directions for 100 random sample -> Merge these directions to Matrix M -> Estimate the common curved directions as m largest singular vectors of M (u1, u2, u3...um).
-> Evaluate the curvature of decision boundary in such direction for poinst z in the vicinity of un
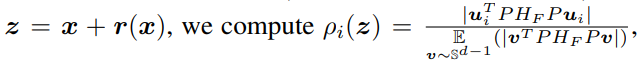
which measures how curved in direction $u_i$
x축: Data point / y축: Curvature