Feature extraction, Image matching, Object recognition
0) Warming up
Computer Vision 에는 크게
- Image Processing
- Geometric Reasoning
- Recognition
- Deep Learning
이렇게 포함된다한다.
Invariant(변하지않는) to view point, lighting, pose 가 좋은 feature이긴 함
1) Convolution 이란?
특정 함수(=커널)을 통해 Input image를 새로운 output image로 변화시키는 것이다.
Input Image f(x,y) Kernel h(x,y) ------> output Image g(x,y)
여기서 쓰이는 convolution kernel은 작은 matrix를 의미
2) Linear filtering 종류
위 커널을 이용해 원본이미지와 결합하여 필터링한다.
- Smoothing: average, bilinear, gaussain 필터링
http://opencv-srf.blogspot.kr/2013/10/smooth-images.html
- Gradient filters : 이미지를 dx and dy방향으로 미분한다. x축 방향으로 변화가 큰 애들이 더 큰 값을 갖게 되므로, 변화량 클수록 더 도드라진다고 보면 된다.
이런식으로 미분 후, Edge를 찾을 때는 0을 중심으로 보고 positive/negative Edge를 찾는다.
Edge Detection은 어떤식으로 이루어지는건지?
-> 위 그라디언트 필터 이용, 보통 smoothing을 통해 좀 평균화를 시키고 미분을 한다. 그러므로 그라디언트 필터 적용하기전에 가우시안 필터 적용하면 더 직관적으로 잘 된다고 한다.
*아래 그림으로 예시가 잘 되있어서 퍼옴 : 출처 http://aishack.in/tutorials/image-convolution-examples/
Simple box blur
Here's a first and simplest. This convolution kernel has an averaging effect. So you end up with a slight blur. The image convolution kernel is:
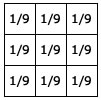
Note that the sum of all elements of this matrix is 1.0. This is important. If the sum is not exactly one, the resultant image will be brighter or darker.
Here's a blur that I got on an image:

A simple blur done with convolutions
Gaussian blur
Gaussian blur has certain mathematical properties that makes it important for computer vision. And you can approximate it with an image convolution. The image convolution kernel for a Gaussian blur is:

Here's a result that I got:

Line detection with image convolutions
With image convolutions, you can easily detect lines. Here are four convolutions to detect horizontal, vertical and lines at 45 degrees:
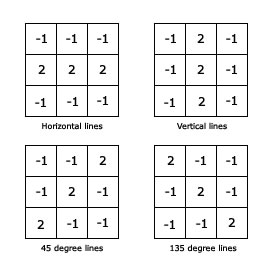 I looked for horizontal lines on the house image. The result I got for this image convolution was:
I looked for horizontal lines on the house image. The result I got for this image convolution was:

Edge detection
The above kernels are in a way edge detectors. Only thing is that they have separate components for horizontal and vertical lines. A way to "combine" the results is to merge the convolution kernels. The new image convolution kernel looks like this:
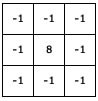
Below result I got with edge detection:

The Sobel Edge Operator
The above operators are very prone to noise. The Sobel edge operators have a smoothing effect, so they're less affected to noise. Again, there's a horizontal component and a vertical component.
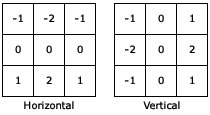
On applying this image convolution, the result was:

The laplacian operator
The laplacian is the second derivative of the image. It is extremely sensitive to noise, so it isn't used as much as other operators. Unless, of course you have specific requirements.
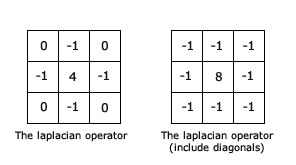
Here's the result with the convolution kernel without diagonals:

The Laplacian of Gaussian
The laplacian alone has the disadvantage of being extremely sensitive to noise. So, smoothing the image before a laplacian improves the results we get. This is done with a 5x5 image convolution kernel.
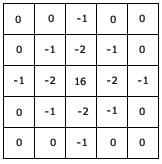
The result on applying this image convolution was:

'IT > Computer vision' 카테고리의 다른 글
| Computer vision - Ransac (0) | 2017.06.29 |
|---|---|
| Computer vision - Sliding window, Detection (0) | 2017.06.29 |
| Computer vision - Blob, SIFT, HOG (0) | 2017.06.29 |